第2课时向量的加减法运算及其几何意义
基础达标
1.对于任意向量a,b,给出下列各式:①a+b=b+a;②+c=b+;③|a+b|=|a|+|b|;④|a+b|≤|a|+|b|.其中恒成立的有.
A.1个B.2个C.3个D.4个
【分析】显然①②④恒成立.
【答案】C
2.若a的终点与b的起点重合,c的起点与b的终点重合,则下列结论中正确的个数为.
①以a的起点为终点,以c的起点为起点的向量为-;
②以a的起点为终点,以c的终点为起点的向量为-a-b-c;
③以b的起点为终点,以c的终点为起点的向量为-b-c.
A.0 B.1 C.2 D.3
【分析】由向量的加减法运算法则可知,①②③均正确,故选D.
【答案】D
3.已知ABCD是四边形,O是该平面内的任意一点,若
+
=
+
,则四边形ABCD是.
A.正方形 B.平行四边形
C.矩形 D.菱形
【分析】由已知,得
-
=
-
,所以
=
,即四边形的对边平行且相等,则四边形ABCD为平行四边形,故选B.
【答案】B
4.下列式子中不可以化简为
的是.
A.
+
+
B.+
+-
C.-
+
D.+-
【分析】A中,++=+
=
;
B中,+=0
+
+
=;
C中,+-=0
+=;
D中,+-=
-=+
≠.
【答案】D
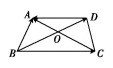
5.如图,在梯形ABCD中,AD∥BC,AC与BD交于点O,则
-
-++
=__________.
【分析】--++
=-+
=
-+=.
【答案】
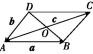
6.如图所示,O是平行四边形ABCD的对角线AC与BD的交点,设
=a,=b,=c,求证:b+c-a=.
【分析】由于b+c=+=+=,+a=+=,所以b+c=+a,即b+c-a=.
由于c-a=-=-=,=+
=-b,所以c-a=-b,即b+c-a=.
7.如图,一架飞机从A地按北偏西30°的方向飞行300 km后到达B地,然后向C地飞行.已知C地在A地北偏东60°的方向处,且A,C两地相距300 km,求飞机从B地向C地飞行的方向及B,C两地的距离.
【分析】由题意和图形可知∠BAC=90°,||=|
|=300 km,则||=300
km.
由于∠ABC=45°,A地在B地南偏东30°的方向处,所以C地在B地南偏东75°的方向处.
故飞机从B地向C地飞行的方向为南偏东75°,B,C两地的距离为300 km.
拓展提高
8.若O,E,F是不共线的任意三点,则以下各式中成立的是.
A.=
+
B.=-
C.=-+
D.=--
【分析】由向量的减法的概念求解可知选B.
【答案】B
9.已知O是△ABC内的一点,且++=0,则O是△ABC的.
A.垂心 B.重心 C.内心 D.外心
【分析】∵+是以,为邻边作平行四边形的对角线,且过AB的中点,设为D,则+=2,
∴2+=0,∴||=
||,故点O为重心,选B.
【答案】B
10.若O是△ABC所在平面内一点,且满足|-|=|-+-|,则△ABC的形状为__________.
【分析】由于-+-=+,-==-,又|-|=|-+-|,所以|+|=|-|,所以以AB,AC为邻边的平行四边形的两条对角线的长度相等,所以此平行四边形为矩形,则AB⊥AC,所以△ABC是直角三角形.
【答案】直角三角形
11.如图,已知正方形ABCD的边长为1,=a,=b,
=c,试作出下列向量,并分别求出其长度.
a+b+c;
a-b+c.
【分析】如图,由已知得a+b=+==c,延长AC至点E,
使||=||,
则a+b+c=,且||=2,
∴|a+b+c|=2.
作=,连接CF,则+=.
∵=-=a-=a-b,
∴a-b+c=+=,且||=2,
∴|a-b+c|=2.
